The 100% success rate of CCCC in problem solving might seem braggadocio or a spate of good luck that is bound to show some failure as soon as enough time is allowed to elapse. Understanding that MOST of the world’s phenomena are based on non-linear transaction or ‘chaos theory’ or ‘emergence’ – just the opposite to the Western world’s intellectual thought development, is demonstrated in one case. CCCC merely applies these chaos fundamentals with its bottom-up approach to problem solving and achieves continuing success – against all odds. And you apply chaos too; you probably don’t know it’s chaos at work because your training and education have been based on the Western mentality that strives for the beauty of hierarchical order. ‘Emergence’, the subject matter of this paper, a new discovery, but as old as creation of the universe itself, will describe the chaos phenomenon – one that profoundly affects every aspect of our lives.
Locusts, Typhoid and Skiers
This early winter of 2005, Africa has been beset with a plaque of locusts, billions of them – that strip every field in which they land clean of food. Why do so many of these creatures emerge unpredictably some years but not others? The exact timing of the cycle of growth and demise of the locusts is not predictable; it’s not as if you can expect the hordes every five years. Yet its recorded occurrence goes back to biblical times.
An equally unpredictable disaster in current world history (i.e. the past millennium) is the typhoid plague. The typhus bacterium emerges and then dissipates only to emerge unpredictably, and catastrophically, a half century, or perhaps, a century, later.
On a ski hill, as I am seeking to conquer a mountain alone. Suddenly a dozen skiers appear who mess up my desire for just Mother Nature and me. A few minutes later I am alone again. A ski instructor at Mont Tremblant, Quebec once described the phenomenon to me as the ‘bus effect’: “You never know what size of group the bus will bring.” Yet the ski lifts operate in an orderly manner, one gondola after another in a completely predictable fashion.
What about earthquakes, tsunamis and weather? Predictable or unpredictable? Chaos theory makes them predictable generally, but not specifically.
I hope to share with you, how chaos is pervasive in our lives and why I and my associates apply its concepts, affectionately called BUM (Bottom-Up Management approach), in all our business development programs. BUM © falls out of our 53 steps for righting the wrongs of the management of human endeavors. The details are described by the recent 12-volume, 2,500 page series on management (1).
Bottom-up or chaotic orders (or disorders) are the antithesis of Western training and especially Western mathematics’ orderly evolution and development.
Slime Mold and Harvester Ants
In his 2001 soon-to-be classic, Emergence (2), Steven Johnson introduces us to slime mold and harvester ants.
He begins his book describing the announcement in August 2000 by a Japanese scientist who had ‘trained’ slime mold, an amoeba-like organism with no centralized brain whatsoever, to find the shortest route through a maze.
Slime mold, a reddish orange mass, will suddenly appear on damp, rotting wood in gardens and forests all around us. The mass moves slowly across the forest floor or, just as suddenly as it appeared, it will disappear. Did it wander elsewhere or did it evaporate? No; it disassembled itself – a behavior that has confounded logical scientists for centuries. Most of the time, slime mold exists as thousands of distinct single-celled units each behaving separately from its neighbors. Then upon some apparent signal or condition the cells come together to form a mass that slowly works itself across the garden floor consuming rotting leaves and wood. It oscillates, depending on the conditions, of being a single cell or a mass of cells.
Recent studies of harvester ant colonies show there is no head organizer. The queen ant is not a leader; she is a baby factory – that’s it. The remaining ants – all female – either harvest or build. The male flies in one day of the year, plants his seeds with queenie and dies. The poor chap is not even equipped with jaws as he does not live long enough to get hungry. Since there is no leader, how do harvester ants go about their duties adjusting to the variables around them? They know how to compute the shortest distance to a food source, how to locate the ant cemetery away from their garbage heap and the preferred distance away from the anthill, how to prioritize food sources based on distance from the nest and ease of access, how to switch worker ants from nest building to foraging – all in response to the external conditions. That is, they engage in improvised problem solving. With minimal cognitive skills, and no one in charge, they respond globally to the needs of the nest. It is this skill of thinking locally, acting locally but with their collective actions producing global behavior that arouses scientific curiosity – just like the slime mold and just like our human cells that manage to work so well together.
Emergence
The term ‘emergence’ has evolved from this observation of a network of self-organization of disparate agents that unwittingly create a higher-level order. The results ‘emerge’ from self-organization that transcends local discipline to solve problems by comparing behavior in one area to behavior in another. That is, the behavior of the group grows smarter over time, responding to the changing needs of the environment. The common features of emergent systems are that they solve problems by drawing on masses of relatively simple elements rather than being organized by any hierarchy. Emergence, therefore is defined as the movement from low-level rules to higher-level sophistication. In a word, it is bottom-up behavior that organizes the final desirable result vs. top-down thinking – decentralized systems vs. centralized systems – “the eerie invisible hand of self-organization”. Within it, a neighbor is influenced by neighbor, which in turn influences back. All emergent systems are built on the two-way feedback, the two-way connection that ultimately fosters higher learning.
Back to the harvester ant’s foraging for food. If a foraging ant notices that most of its neighbors are also foraging, it make the decision to switch its role to nest building (and care of infant ants). It picks up this information only from the neighboring ants. If there is an equilibrium between the number of foragers and nest builders that it sees, the ant continues as is – a simple binary [0, 1] decision for the ant. “If there is an equilibrium, more or less, I continue as I am; if there are too many doing what I am doing, I will switch my role to the other one.” There is no examination of the global picture but simply a response to local conditions. This decision has another factor – area. The ants operate within a few meters of their nest. If they were to all forage far beyond it, they would not meet many of their neighbors and not react to any change in external circumstances. (This has the implication as you will see later in the ‘extinct’ phase of chaos.)
Orderly Mathematicians
For good reason we humans make an effort to create order out of disorder. We attempt to compartmentalize and organize information so that we can remember or process it more easily. We establish and welcome hierarchies for things. Even abstract thinkers such as theoretical mathematicians do this. If there is not a hierarchy, we tend to create one. For example, most of humankind assumes that the world was created by a great spiritual leader – it could not just have appeared on its own. So when an ancient mathematician, such as Euclid, invented geometry 2,500 years ago, thereby creating order for shapes, we were quick to embrace it and do so to this day. But think for a minute: most shapes of most things in this world are not neatly round, not neatly square and not neatly triangular – stones, shorelines and storm fronts. Euclid’s rules cover only a tiny aspect of the environment’s shapes. Yet it is the authority of shapes taught in almost every high school in the world. This quest for order extends to higher level mathematicians in their association with the study of atomic particle movement, economics, population development of men and mice, etc. When the actual results vary with pure formulae, the mathematicians have tended to dismiss such chaotic results as anomalies and return to the orderly portions of their calculations.
The Secret Society
It has now been realized that this science or study of order and disorder has been ongoing for centuries if not millennia, but only in the past 30 years has it come together in the West (although it has been hidden behind the Iron Curtain in Russia for at least 20 years before that). It has been secret only inasmuch as people thinking this way have been working independently at it, without connecting to one another.
For example, a young Dr. Mandlebrot, a pivotal developer of chaos theory and applications (3), was invited as a guest lecturer to Harvard to discuss the economics of income distribution. When he arrived at the university he saw upon a blackboard his income distribution formulae. He asked his host: “How did my formula get here before I did?” “That’s not your formula; it’s 8 years of cotton prices” replied the more senior professor. “It has nothing to do with income distribution.” Here then were two mathematicians confronted with the same equation for what appeared to be very different matters. Both had come to the same conclusion about fairly disorderly (or unpredictable) situations. The common element is that they both dealt with chaotic phenomena.
In the 1960’s, Alan Turing who played a large role in the inventor of the digital computer (and was the astounding code-breaker from World War II) worked out a mathematical model wherein simple agents follow simple rules to generate amazingly complex structures. He called it “Pandemonium”. The secret was let out of the bag.
The secret really exploded out of the bag in an understandable way when Dr. Edward Lorenz, a meteorologist, described the Butterfly Effect in 1972 with the idea of a butterfly flapping its wings in the Amazonian jungle today causing a storm a week later in Texas. He supported his postulates with a set of equations and numerous examples. Today the Butterfly Effect has been applied to explain how cities evolve to take on certain shapes for the location of factories, retailers, low income people, high income people, etc., a New York City measles epidemic, 200 years of fluctuation of the Canadian lynx population as recorded by trappers of the Hudson Bay Company, other disorderly disease cycles such as for polio, rubella, gonorrhea to name a few.
The Formula for Chaos
Much of current-day mathematics tends to deal with linear equations with things rising as the pressure or attention to them increases. It is the non-linear equation that leads to disorder: xnext = px(1-x). While you may or may not appreciate the differences between the two types of equations, the real interest is that after a while the non-linear equation appears to get out of control. In the past, many mathematicians glossed over this chaotic phase and worked on either side of it. There are several stages for the non-linear equation.
In stage 1 nothing happens. The y axis does not rise with the initial stimulant; the species appears extinct, or the ants, being so far apart do not change their behavior, or the slime mold remains as individual cells.
In stage 2, there is a growth in an orderly fashion, proportional, more or less, to the stimulus – as you would expect. The more you turn up the thermostat, the more people that leave the room.
Suddenly in stage 3 the rising line divides in two. Then it divides in two again, paralleling cell growth multiplication in the embryo.
Then stage 4 arrives – chaos – and uncontrollable multiplication – the locusts, the lemmings and the nuclear reaction that leads to an atomic explosion. Other than these more common phenomena, scientist tend to jump past this chaotic anomaly and move onto stage 5.
In stage 5 there is a return to normal cyclical behavior such as population doubling every 7 years (although the actual cycle time is not predictable – it could be every 3 years or every 29 years), the doubling bifurcation (as in Stage 3) combines with cycles such as 3, 6, 12 etc.
Then stage 6 represents the re-establishment of chaos.
The repetitive chaos of the sixth stage supports the recent, controversial, scientific postulation that our universe is but one of a cycle of universe creations and destructions (5).
These stages have been sketched clearly by James Gleick in Chaos, pages 73 and 74 (3). Our representation is our follows:
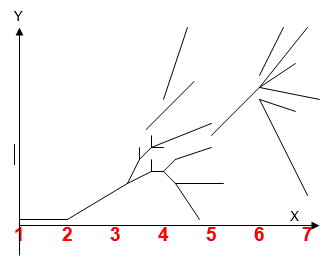
Applications of Chaos
One way of stating what chaos theory is about is to say that a number of insignificant events, often appearing to be unconnected, can lead to a major or significant event. The only qualification to the major event is that one cannot predict the where, the when, the who and the how of the major event.
(a) From the point of view of practical fun, recently, chaos has been applied to computer games that build solutions by unpredictable emergent principles, following very simple rules like the harvester ants.
(b) A current crochet piece was developed causing a stir not only with its beauty but also with the realization that its 25,511-stitch structure (aptly named the Lorenz Manifold) had its stitches formed chaotically moving from one wing of the structure to another in an unpredictable way (4).
(c) A hockey goalie will, on average, turn away 10 to 20 shots before allowing one puck to get in, even when faced with professional hockey players roaring down the ice with great intent. That is, a professionally-skilled hockey player on a one-to-one confrontation with a goalie will lose most of the time. The coaches, recognizing this fact, unknowingly revert to chaos theory in order to increase the odds of their teams scoring on the opponents. They instruct their players to ‘go to the net’. So, 3 or 4 players will position themselves in front of the net, fighting for space there against their counterparts, bashing the puck around back and forth until it careens off someone or something and goes into the net to score a goal. It can bounce off a shoulder, a skate or even a protective defenseman – who knows what or who?
For that reason coaches tell their charges: “Good things happen when you go to the net!”
In this example, the unconnected minor events are the players moving the puck around, back and forth without a plan other than to keep the puck moving and to bash it into the net at any chance. The major or significant event is the goal being scored. The unpredictability is that no one can say beforehand who will score the goal and how it will go in.
(d) Cities, as noted before, will evolve by themselves without central planning (except for a chosen few capital cities such as Brasilia) into districts of retail, districts of fabrication, districts according to income distribution, and so on. This formation is predictable from chaos theory. The unpredictable portion is how this arrangement will finally pan out for the city. Thus, the final layout of Manchester England is quite different than that of Philadelphia but both share the same predictable regions.
(e) For the past 8 years I have applied chaos theory to commercial problem solving. The process starts by accumulating information, from a group of people seriously affected by the problem, in a random and thus, disorderly fashion – any idea, any thought, important or trivial, hurts and joys, etc. (1). Participants accustomed to orderly processes are disturbed by the approach that seems to be leading nowhere and even try to thwart it by developing top-down suggestions instead of going along with this bottom-up management strategy. Of course, it is exacerbated for them because the posting of so many thoughts stimulates the creation of even more thoughts. These resisting people may attempt to organize the data before the accumulation has been completed. We tell them to hold on till we’re done. With the build up of a hundred or more thoughts now before the group, we then move onto an organizing of the information, not by a planned route but by allowing the pieces of information themselves to tell us how to form the structure. For example: “Many of these thoughts are about time frames, so let’s group all the time-related ideas together. Quite a few of the concerns have a financial connotation, so let’s put these financial ones into the same column. If a thought spans both orders, then let’s place it in both.” Each of the original ideas or thoughts are placed onto sticky notes, because if the first order doesn’t seem to work, we are open to shifting it towards another order quickly – which the sticky notes facilitate. The first order creates a path to a further order in exactly the same way. It also stimulates more thoughts and concerns and each such new idea is explored so new stickies are added to the accumulations for sorting as well. Then the order converges and converges until a solution appears – a beautiful solution because everyone in the room sees its elegant practicality. That solution is unique to the situation based on all the preliminary information – which is, at the end, tested against it. There is an unanimous consent – a solution without compromise, the epitome of the 100% success rate – thanks to a chaotic start. No one, not even an experienced facilitator, could have seen the solution in advance.
(f) In the past year I have been involved in – peripherally at first, intently at present – in helping people find jobs via the route of the unpublished or hidden job market where about 75% of new jobs lie. Since they’re hidden, the challenge is to find them. There is no predictable path, only a predictable method. We begin by peeling back the curtain that exposes the hidden job area by having the candidate talk with personal acquaintances. Understand that many of these candidates are new to the city. “I have no friends or contacts here; I don’t know where to start.” We start chaotically, i.e. with a simple unplanned path – his sister, his insurance agent and his neighbor. These lead us to a new level of contacts and by the third iteration we are seeing signs of jobs in the candidate’s area of expertise. By the sixth iteration we hone in on one or more ideal job choices – ones that provide a thrill, not a struggle for candidates. (We have developed statistical histograms that show medians and distributions for contacts, but that gets too technical for the intent of this paper.) The point is that we don’t know where we are going or exactly how it will end up with our ‘local-first’ approach but it leads to a global result – the finding of a job in the specialist’s desired field. We process many professionals – engineers, PhD’s, scientists and software developers – in bad times and in good, always with remarkable results. (When people follow the chaotic route we espouse, I believe we have a 100% success rate. One has to decide if a candidate is really following the rules and if the time frame is appropriate to confirm the 100%.)
Summation
Chaos is much more prevalent in the world than order, so its implications should not be ignored. In fact, they should be embraced since they explain far more common phenomena than do orderly approaches.
Bill Caswell
